数学関連の記事
 和算
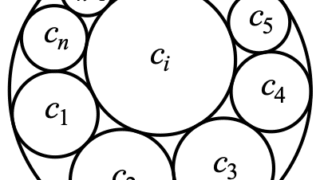
和算 算変座標とシュタイナー円鎖
これは2023年10月の論文です
松山大学創立100周年記念論文集, (2023) pp. 51--72.
論文の「はじめに」の部分を引用して論文紹介とします。
算変座標は、複数の円が互いに接している和算問題への...
 和算
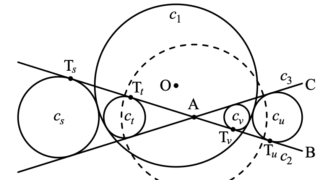
和算 算変座標の基礎(2)
これは2024年4月の論文です。
松山大学論集 第36巻第1号, (2024) pp. 61ー126.
論文の最初の「はじめに」の部分を引用して論文紹介とします。
算変座標は論文「算変法不変式がつくる座標系につい...
 和算
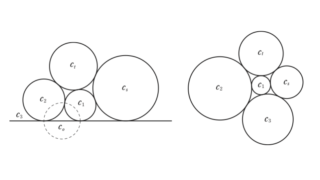
和算 算変座標の基礎(1)
これは2023年8月の論文です。
松山大学論集 第35巻第3号、(2023) pp. 19ー72
論文の最初の「はじめに」の部分を引用して論文紹介とします。
算変座標は論文「算変法不変式がつくる座標系について」で...
 お知らせ
お知らせ 愛媛和算研究会ホームページ開設
愛媛和算研究会がホームページによる情報発信を開始しました。
研究会が発足してから今年で25年になります。
四半世紀かけて研究してきた成果を集めたホームページとして、愛媛の算額や和算書に関する情報が満載です。
是非立ち寄っ...
 和算
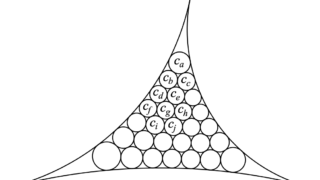
和算 算変座標の杉成算への応用
これは2023年2月の論文です。
松山大学論集 第34巻第6号, (2023) pp. 51--89.
和算の問題に杉成算というものがあります。
【杉成算】互いに接する3円 \(c_1,c_2,c_3\)(半径をそれ...
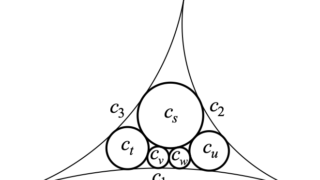 和算
和算 算変法不変式がつくる座標系について
久々の投稿です。一昨年の2022年4月に発表した論文がようやく松山大学リポジトリに登録されました。その論文を紹介します。
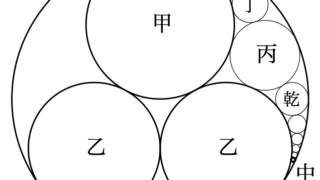
上の図はこの論文の例題4として取り上げた問題です。
【問題】互いに接している3円 \(c_1,c_2,c...
 和算
和算 散歩と研究会発表
午前中に1時間少々散歩しました。いつもは地面を歩くだけなのですが、今日は歩道橋にも登ってみました。
歩道橋からの景気はいつもの視線とは違っていて新鮮だったので、写真も撮ってみました。
午後は日本数学...
 和算
和算 数学史研究発表会
今日は日本数学史学会の研究発表会が zoom であり、私も研究発表をしました。
タイトルは「『累円術無寄』について ー算変座標で解くー」です。
反転法や算変法を発展させた、算変座標という座標系を用いて、和算の問題を解いてみると...
 和算
和算 全国和算研究大会秋田大会に参加してきました
2022年11月5日(土)・6日(日)の2日の日程で「第18回全国和算研究大会秋田大会」が秋田市のにぎわい交流館で開催され、それに参加してきました。
コロナの影響で2020年と2021年は大会が中止だったので、待ちに待った待...
 折り紙の数学
折り紙の数学 準正多面体を作ってみよう
正多面体のことはよく知っていると思います。
正四面体、正六面体(立方体)、正八面体、正十二面体、正二十面体 の5つです。
では、準正多面体とはどんな立体なのでしょうか。
異なる種類の面、(例えば、正三角形、正方形、正五角...