折り紙の数学 錐体の体積公式と等高重心立体に関する考察
2018年の論文です。日本数学教育学会高専・大学部会論文誌 24-1 (2018) pp.1--14 に載りました。
球・円柱・円錐のような立体図形は、平面上を滑らかに転がります。これらの立体は、転がしても常に重心の高さが一定です。...
数学
折り紙の数学 
数学 網代編みの対称性
竹の編み方に「網代編み」という編み方があります。パターンは2種類あって、上の図が「2本とび網代編み」で、下の図が「3本とび網代編み」です。
3本とび網代編み
対称性を調べてみると下の図のように、180°の回転対称の中心（青色の...
折り紙の数学 多面体と展開図における半分長定理について
2016年の論文です。日本数学教育学会高専・大学部会論文誌 22-1 (2016) pp.27--38 に載りました。
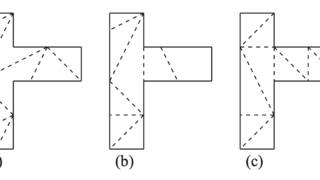
凸多面体から展開図を作る問題の逆問題として、平面図形（平面多角形）から凸多面体を作る問題があります。
展開...
数学 亀甲編みの対称性
竹の編み方に「亀甲編み」という編み方があります。
この編み方をパターン化したものが上の図です。
対称性を調べてみると下の図のように、60°の回転対称の中心（水色の六角星）、120°の回転対称の中心（オレンジ色三角形）、180°...
数学 ござ目編みの対称性
竹の編み方に「ござ目編み」という編み方があります。
この編み方をパターン化したものが上の図です。
対称性を調べてみると下の図のように、180°の回転対称の中心（青色の丸印）があり、さらに鏡映軸（赤い実線）が縦横2方向あり、その...
数学 四つ目編みの対称性
竹の編み方に「四つ目編み」という編み方があります。
この編み方をパターン化したものが上の図です。
対称性を調べてみると下の図のように、90°の回転対称の中心（緑色の四角）、180°の回転対称の中心（青色の丸印）があることがわか...
和算 田中民部介と和田栄太郎の算額
2017年の論文（共著）です。日本数学教育学会高専・大学部会論文誌 23-1 (2017) pp.77-90 に載りました。
この論文では、田中民部介の算額と和田栄太郎の算額を取り上げました。これら 2 つの算額はどちらも現存しませ...
数学 六つ目編みの対称性
竹の編み方に「六つ目編み」という編み方があります。
この編み方をパターン化したものが上の図です。
対称性を調べてみると下の図のように、60°の回転対称の中心（水色の金平糖）、120°の回転対称の中心（オレンジ色三角形）、180...
和算 大西佐兵衛と小嶌又兵衛の算額
2016年の論文（共著）です。日本数学教育学会高専・大学部会論文誌 22-1 (2016) pp.15-26 に載りました。
この論文では、伊佐爾波神社に 1803 年に奉納された大西佐兵衛の算額と1812 年に奉納された小嶌又兵衛...
和算 山崎喜右衛門と栗林佐太郎の算額
2015年の論文（共著）です。日本数学教育学会高専・大学部会論文誌 21-1 (2015) pp.1-14 に載りました。
算額は数学の問いと答えを額にして神社仏閣に奉納したもので、江戸時代から明治にかけて算額の奉納がさかんに行われ...