久々の投稿です。一昨年の2022年4月に発表した論文がようやく松山大学リポジトリに登録されました。その論文を紹介します。
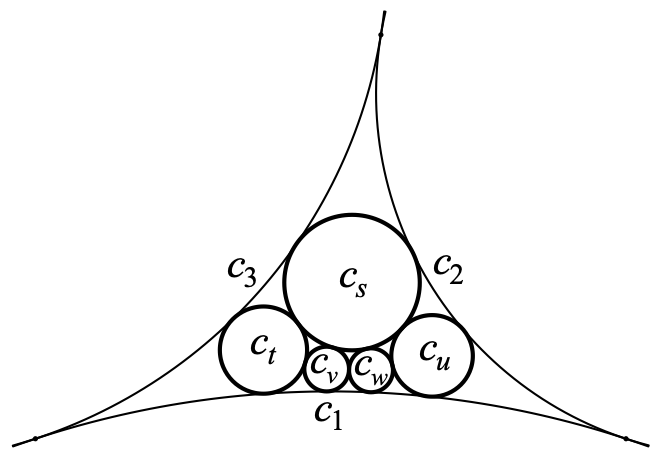
上の図はこの論文の例題4として取り上げた問題です。
【問題】互いに接している3円 \(c_1,c_2,c_3\) の半径 \(r_1,r_2,r_3\) が与えられている。その3円で挟まれた領域に5円 \(c_s,c_t,c_u,c_v,c_w\) を図のように容れるとき、5円の半径を求めよ。
和算の問題によくあるものですが、この種の問題は難問です。
そこでこの論文では、円の位置と半径を決定するための「算変座標」という座標系を定義しました。
5円を算変座標で表し、2円が接するという条件を方程式で表し、接点の数だけ方程式を作ります。その連立方程式を解くことにより5円の半径を求めようというものです。
論文では、算変座標を定義し、その性質について述べ、さらに、2円が接する条件を導く距離公式、算変座標が決まったら円の半径を求める半径公式、などを導いています。
その応用としては、上の問題を含む5つの例題を取り上げ、距離公式や半径公式の使い方を紹介しています。
算変座標は和算の問題の中で多数の円が接している問題の解法に役立つものと思っています。
論文はここからダウンロードできます。