今日は日本数学史学会の研究発表会が zoom であり、私も研究発表をしました。
タイトルは「『累円術無寄』について ー算変座標で解くー」です。
反転法や算変法を発展させた、算変座標という座標系を用いて、和算の問題を解いてみるという研究です。
ことの発端は、先月の全国和算研究秋田大会で研究発表を行ったときのことです。発表の最後に「秋田に来る前に鳴海風先生の『遊歴算家・山口和「奥の細道」をゆく』を読んでいたのですが、その挿絵にあった和算問題を算変座標で解いてみたら、簡単に解けました、でもなぜか答えは合いませんでした」と余計なことを言ってしまったことがこの研究の発端になりました。
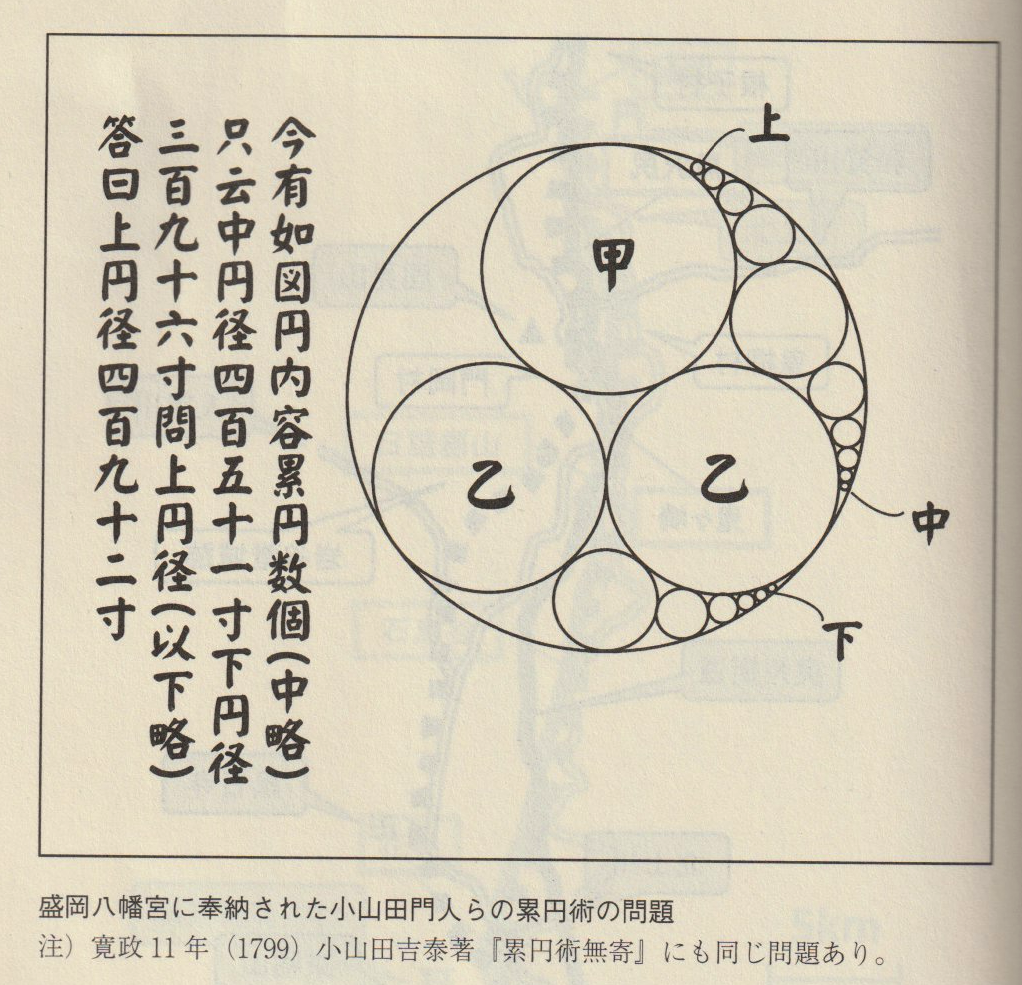
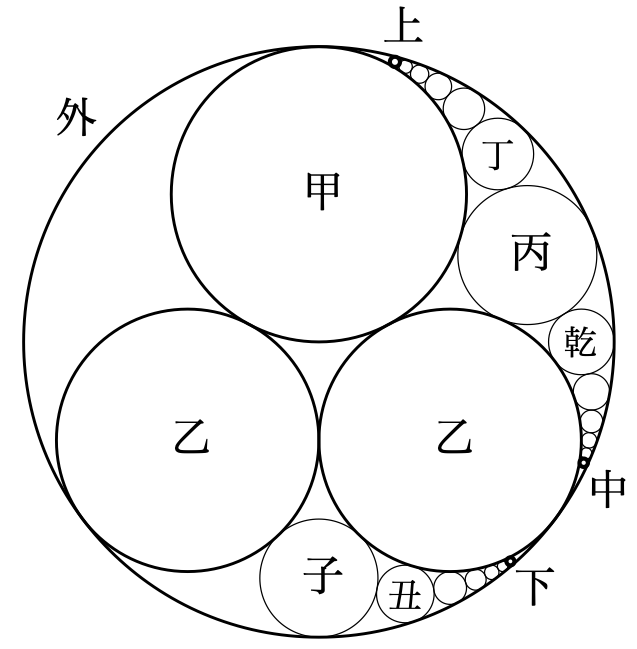
その本の挿絵にあった説明では一部が(中略)、そして(以下略)となっている箇所があって完全な問題が書いてなかったので、問題文を間違えて解釈してしまったのが原因で、そのため答えが合わないという結果となってしまいました。
そこで『累円術無寄』の原文を入手してみると、省略されていた部分にかなりの説明が書いてありました。
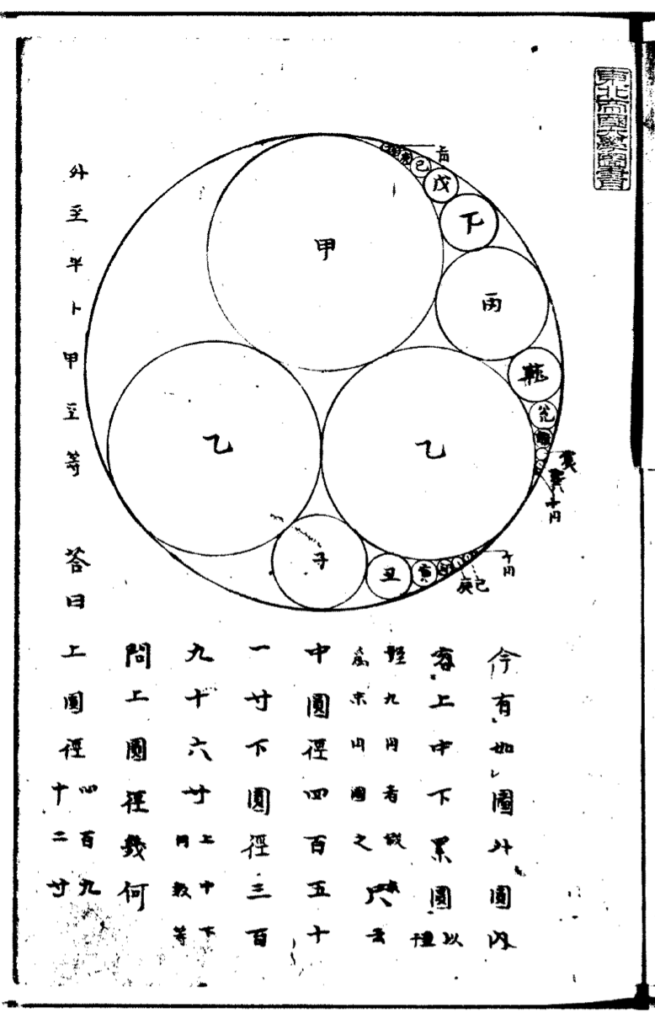
きちんと読んでみると問題設定が挿絵で見たのとはだいぶ違っていました。もう一度計算し直してみたら、和算書の答と私の計算結果とが一致しました。これは先月の失言を撤回しないといけないと思い、研究発表となりました。
その発表資料は論文として掲載されました。数学史研究 第III期 第1巻 第3号 (2023) pp. 117-120。ここからダウンロードできます。
その発表も無事終了したので、今日は飲みます。

肴はモンゴウイカと秋田の比内地鶏のパストラミで、お酒はフランス産のスパークリングワインです。