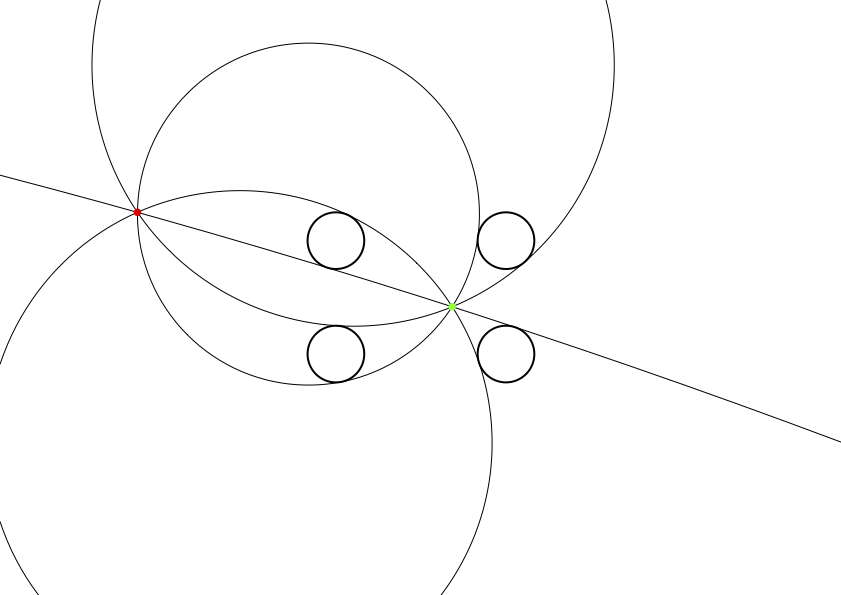
上の図は,赤い点を通り,小さい4つの円の2つに接するように,4通りの円を書いてみたらそれらはみな緑の点で交わりました。不思議ですね。
この図の書き方を順を追って説明します。
最初に小さい4円を書きます。そのときの条件は,(1) 4円の中心を結ぶと長方形となる,(2) 4円の半径はすべて等しい,(3) どの2円も互いに外部にある,です。さらに,その4円の外部に赤い点をとります。

赤い点を通り2円に接する円を,下の図のように4通り描きます。
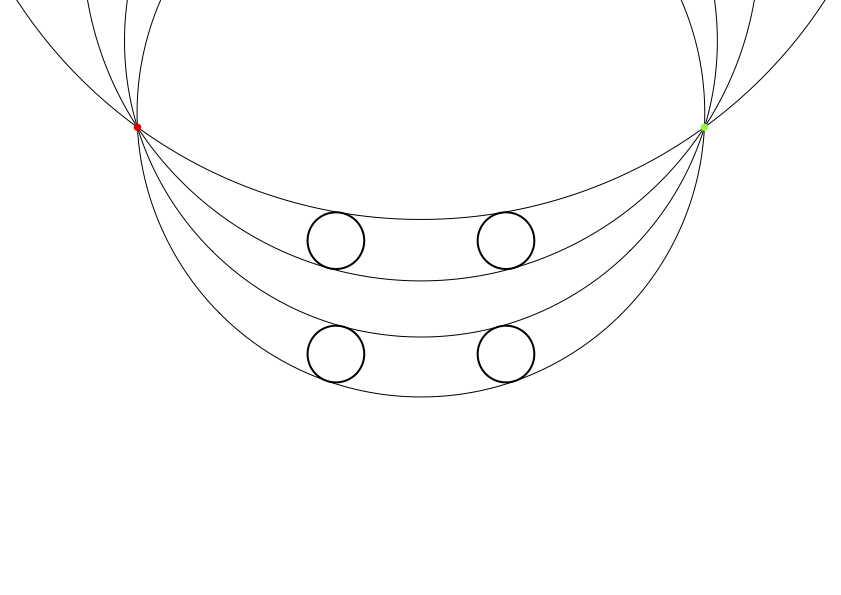
そうすると,これら4通り円はすべて緑の点を通ります。
別の方法で4通りの円を描いてみます。

今度も,4通りの円はすべて緑の点を通ります。
図 2 は鉛直方向の直線に関して線対称なので,緑の点で4つの円が交わることは納得できます。
図 3 についても,今度は水平方向の直線に関して線対称なので,4つの円が緑の点で交わることは納得できます。
さて,もう一つの図です。これも赤い点を通り2円に接する円を,4通り描いています。
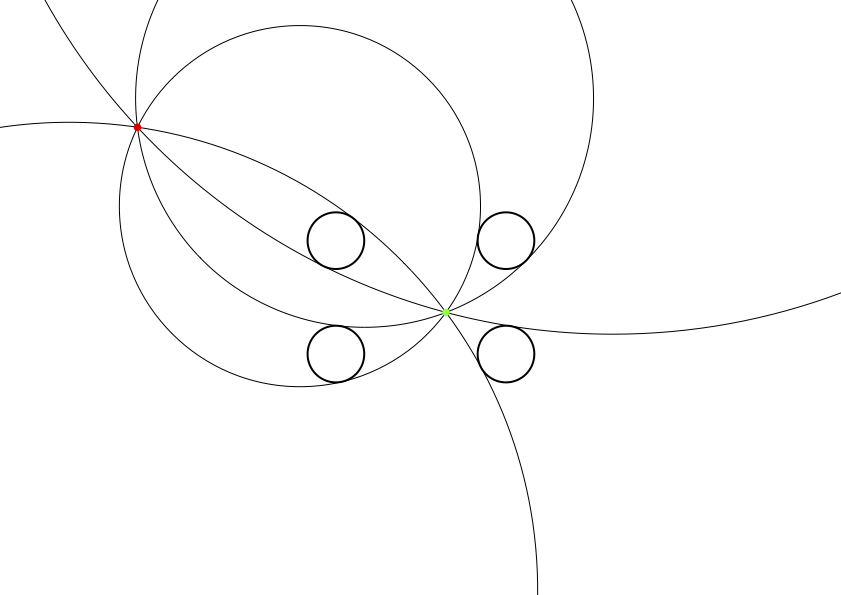
今度はどうでしょうか。4通りの円を描いてみると,やはりすべて緑の点をとおります。
偶然かな? と,思い,赤い点を移動させてみますが,やはり1点で交わっています。

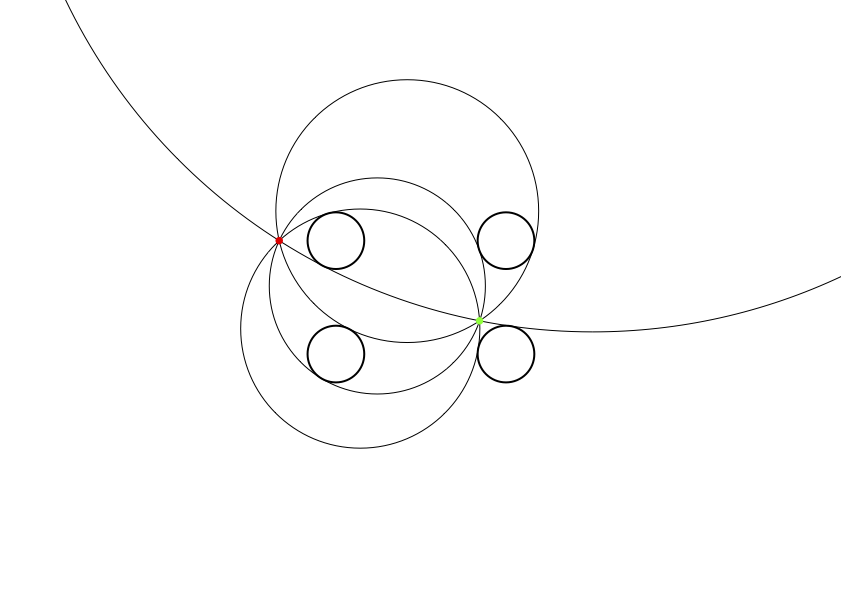
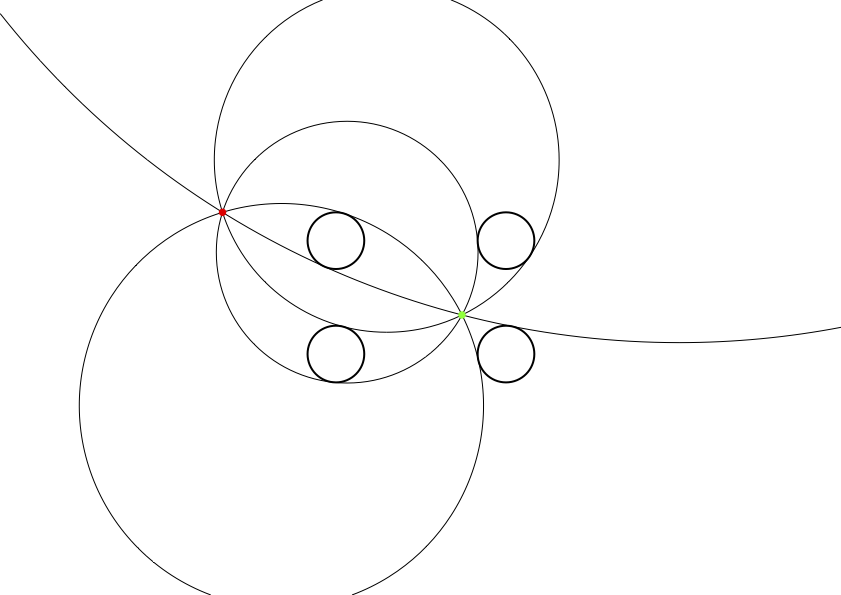
不思議ですね。


