これは2024年4月の論文です。
松山大学論集 第36巻第1号, (2024) pp. 61ー126.
論文の最初の「はじめに」の部分を引用して論文紹介とします。
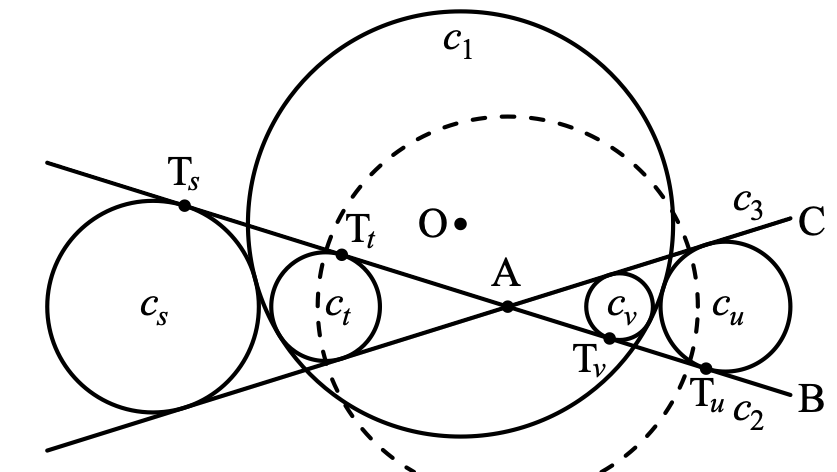
算変座標は論文「算変法不変式がつくる座標系について」で導入した円の幾何学における座標系である。その座標系は和算の問題への応用に適していて,これまで3編の論文で応用例を紹介している。「算変座標の杉成算への応用」では杉成算の問題を扱い,\(n \leq 7\) の範囲で算変座標による解法を示した。「『累円術無寄』について ー算変座標で解くー」では放物型円鎖に関する公式を紹介し,実際に幾つかの例題に応用した。「算変座標とシュタイナー円鎖」ではシュタイナー円鎖についての公式を紹介し,ここでも例題への応用を述べた。
算変座標はその広い応用が期待されるため,算変座標の拠り所となる基礎理論の構築もまた重要な研究テーマとなる。そこで論文「算変座標の基礎(1)」では,基準3円 \(c_1,c_2,c_3\) の基準距離 \((e_1,e_2,e_3)\) が \(\sigma > 0\) をみたす場合について基礎理論の構築を行なった。具体的には,任意の基準距離に対して基準3円が常に存在すること,基準距離が等しい2組の基準3円は一般メビウス変換で移り合うこと,算変座標に対して有向円が存在するための必要十分条件などを明らかにした。距離公式についてはその証明を与え,半径公式については取り扱いやすくするため公式自体を整理し直した。
本論文はその続編として,基準3円 \(c_1,c_2,c_3\) の基準距離 \((e_1,e_2,e_3)\) が \(\sigma < 0\) の場合について,算変座標の基礎理論を構築することが目的である。
この論文はここからダウンロードできます。