これは2023年2月の論文です。
松山大学論集 第34巻第6号, (2023) pp. 51–89.
和算の問題に杉成算というものがあります。
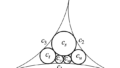
【杉成算】互いに接する3円 \(c_1,c_2,c_3\)(半径をそれぞれ \(r_1,r_2,r_3\) とする)に挟まれた領域に、円を上から順に1個、2個、3個、… と容れ、一番下が \(n\) 個とする。このとき、一番上の円 \(c\) の半径 \(r\) を \(r_1,r_2,r_3,n\) で表せ。(下の図は \(n=4\) の場合で、上の図は \(n=7\) の場合である。)

3円に挟まれた領域に入る \(\frac{n(n+1)}{2}\) 個の円の半径がみな異なっていることがこの問題を難しくしている。
和算家によりこの問題の一般解は
$$ r = \frac{r_1 r_2 r_3}{2 k_n \sqrt{r_1 r_2 r_3 (r_1 + r_2 + r_3)} + k_n^2 r_1 (r_2 + r_3) + r_2 r_3} $$
の形をしていることが知られていました。ただ、 \(k_n\) の値をどのように計算するかが問題でした。
この \(k_n\) の値の計算については \(n = 4\) までについては和算家が色々計算しています。ただ、計算結果には食い違いがありました。また、一般解 \(k_n\) については漸化式を予想してもいました。
その後、岩田至康が1986年の論文で \(n=5\) までを計算し、北原勲が2012年の論文で \(n=6\) までを計算しています。
この問題に算変座標による計算で取り組んでみたのがこの論文です。
算変座標の立場からは、2円 \(c_1\) と \(c\) の反転距離を \(s_n = s(c_1, c)\) とするとき、上の公式は
$$ r = \frac{2 r_1 r_2 r_3}{2 \sqrt{2(s_n + 1) r_1 r_2 r_3 (r_1 + r_2 + r_3)} + (s_n + 1) r_1 (r_2 + r_3) + 2 r_2 r_3} $$
となります。また、\(s_n\) と \(k_n\) の間には \(s_n = 2 k_n^2-1\) という関係があります。
算変座標を使った結果 \(n=7\) まで計算できました。
\(s_n\) の値については
$$ s_1=1, \quad s_2=3, \quad s_3=2\sqrt{2} + 2, \quad s_4=2\sqrt{3}+3 $$
なのですが、その後は3次方程式の解となります。\(s_5\) の近似値は \(7.93735\) で正確には3次方程式
$$ x^3 – (4\sqrt{2} + 5)x^2 + (8\sqrt{2} + 7)x + 12\sqrt{2} + 9=0$$
の解となります。同様に \(s_6\) の近似値は \(9.27763\) で3次方程式
$$ x^3 + (6\sqrt{2} – 20)x^2 + (125 – 76\sqrt{2})x + 198\sqrt{2} – 250=0$$
の解となり、\(s_7\) の近似値は \(10.50821\) で3次方程式
$$ \begin{eqnarray}529x^3 – (7309 + 4392\sqrt{2} + 2802\sqrt{3} + 1508\sqrt{6})x^2 \\ + (64355 + 47072\sqrt{2} + 37408\sqrt{3} + 23416\sqrt{6})x\\ – 218819 – 136256\sqrt{2} – 116350\sqrt{3} – 91212\sqrt{6}=0 \end{eqnarray}$$
の解となります。
残念ながら、\(n=8\) については連立方程式を立てることはできましたが、数式処理ソフトを用いても厳密解を求める(\(s_8\) を解とする方程式を決定する)ことができませんでした。
近侍解でよいのであれば、\(n\geq 8\) に対しても計算は可能です。論文には \(n \leq 15\) までの近似解の計算結果をつけています。
論文はここからダウンロードできます。