2018年の論文です。日本数学教育学会高専・大学部会論文誌 24-1 (2018) pp.1–14 に載りました。
球・円柱・円錐のような立体図形は、平面上を滑らかに転がります。これらの立体は、転がしても常に重心の高さが一定です。
このように、転がしても重心の高さが常に一定である立体を等高重心立体といいます。等高重心立体は、これまで、スフェリコンやヘキサ・スフェリコン等わずかしか知られていませんでした。
この研究のきっかけは、和算書『精要算法』に記されていたある体積公式でした。角錐・円錐等の錐体の体積を求める公式「底面積×高さ÷ 3」は、通常は底面が平面上にあるときに用いられます。
しかし、その和算書では、円錐の側面を底面とする錐体に対してその公式が使われていました。底面が曲面の場合であっても公式が成り立つ場合があることを和算家が知っていたことに驚かされました。
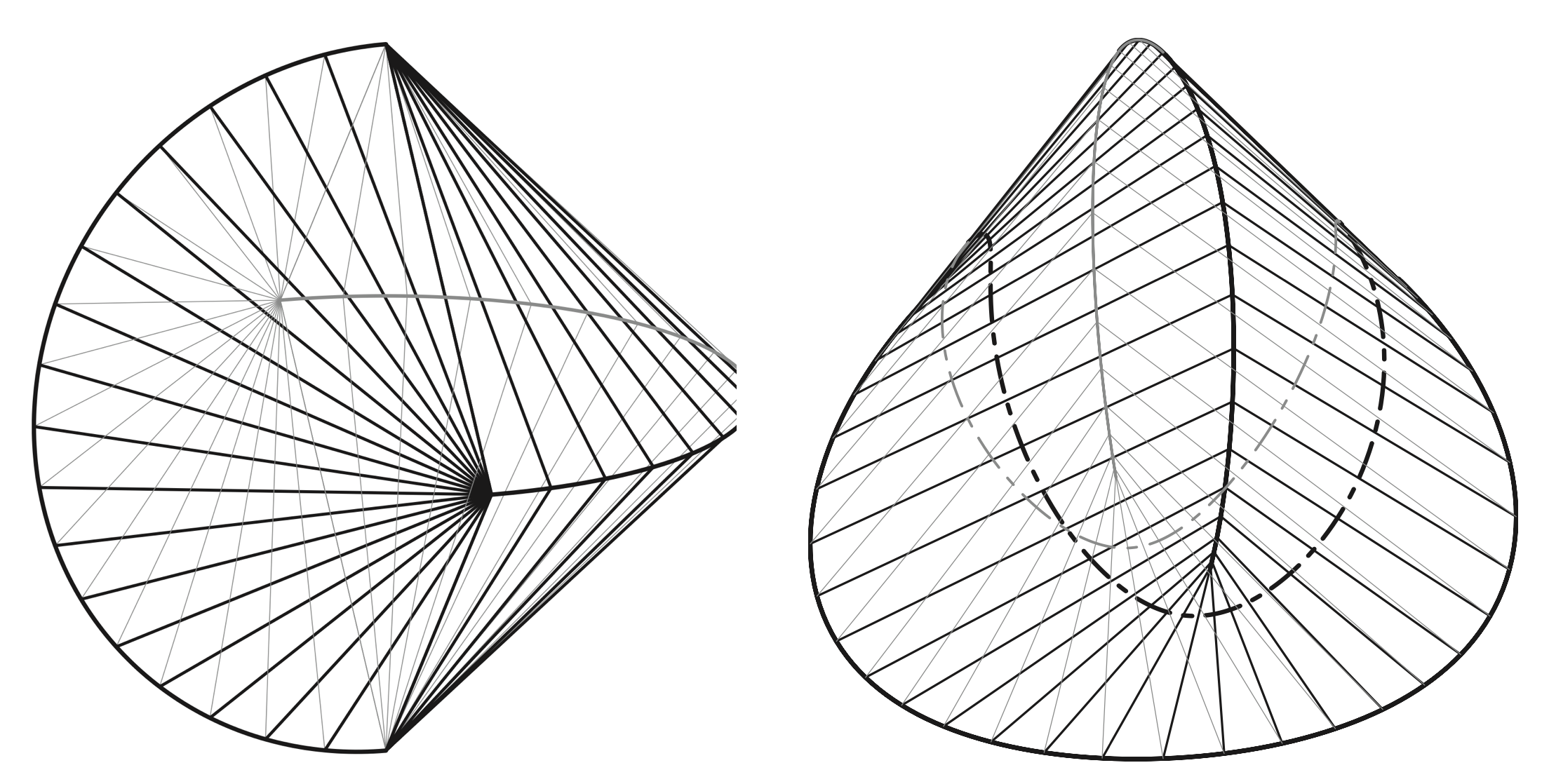
そこで、底面が曲面の場合の錐体で、同様な体積公式が成り立つものが他にもあるだろうと予想して、研究してみることにしました。その結果、以下のような方法で生成した曲面 \(F_c\) に対して、錐体の体積公式が成り立つことが判明しました。しかもそのような曲面は無数に存在することも分かりました。
【曲面の生成方法】 球面 \(S^2\) 上に滑らかな曲線 \(C\) を描く。曲線 \(C\) 上の点 \(x\) における球面の接平面を \(\pi_x\) とする。点 \(x\) を曲線 \(C\) に沿って動かすとき、接平面 \(\pi_x\) のなす包絡面を \(F_c\) とする。
このようにして作られた曲面 \(F_c\) と球の中心 \(\mathrm{P}\)、球の半径 \(h\) に対して次のような体積公式が成り立ちます。
「曲面 \(F_c\) 内の任意の領域 \(X\) に対して、\(X\) と点 \(\mathrm{P}\) とで作られる錐体を \(\mathrm{P}X\) とし、\(X\) の面積を \(S(X)\)、\(\mathrm{P}X\) の体積を \(V(\mathrm{P}X)\) とすれば $$V(\mathrm{P}X) = \frac{1}{3}hS(X) $$ が成り立つ。」
さらに、包絡面\(F_c\) が立体図形を囲む場合は、囲まれる立体を \(P_c\) と表すことにすると、等高重心立体に関して次のような結果が得られました。
「球面 \(S^2\) 上に描く曲線 \(C\) が滑らかな閉曲線で、かつ点対象等のある種の対称性を満たせば、立体 \(P_C\) は等高重心立体である。」
このような曲線 \(C\) は無数にあるので、等高重心立体 \(P_c\) も無数にあることが明らかになりました。
次のリンクから論文を見ることができます。