これは2023年8月の論文です。
松山大学論集 第35巻第3号、(2023) pp. 19ー72
論文の最初の「はじめに」の部分を引用して論文紹介とします。
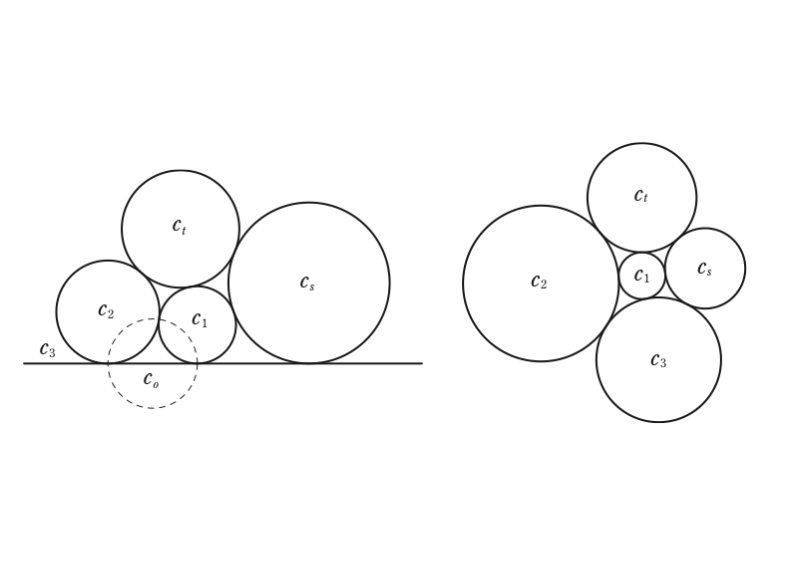
算変座標は論文「算変法不変式がつくる座標系について」で導入した円の幾何学における座標系である。平面 \(E^2\) に無限遠点を加えた \(E_{\infty}^2\) には反転により生成される一般メビウス変換群が作用する。また \(E_{\infty}^2\) 上の2つの有向円 \(c_1, c_2\) に対して一般メビウス変換で不変な値として反転距離 \(s(c_1,c_2) \in R\) が定義できる。これらをもとにして,基準3円と呼ばれる3有向定円が与えられたときに,任意の有向円から基準3円までの反転距離でもって円の座標としての算変座標を定義した。さらにその座標系における基礎公式として半径公式と距離公式を導くことにより,その算変座標は一般メビウス変換で不変な座標系であるだけでなく,円の幾何学を考える上での重要なツールとなることを紹介した。
論文「算変座標の杉成算への応用」では基準距離が \((1,1,1)\) である基準3円についての基礎理論を展開するとともに,和算の中でも難問として知られる杉成算の問題に算変座標の理論を用いることで,\(n=7\) の場合の杉成算を解くことができた。また「『累円術無寄』について -算変座標で解く-」でも算変座標が和算の問題に有効であることを示した。
この論文では基準3円 \(c_1,c_2,c_3\) の基準距離 \((e_1,e_2,e_3)\) が \(\sigma > 0\) をみたす場合について,算変座標の基礎理論を構築することが目的である。
この論文はここからダウンロードできます。