2016年の論文です。日本数学教育学会高専・大学部会論文誌 22-1 (2016) pp.27–38 に載りました。
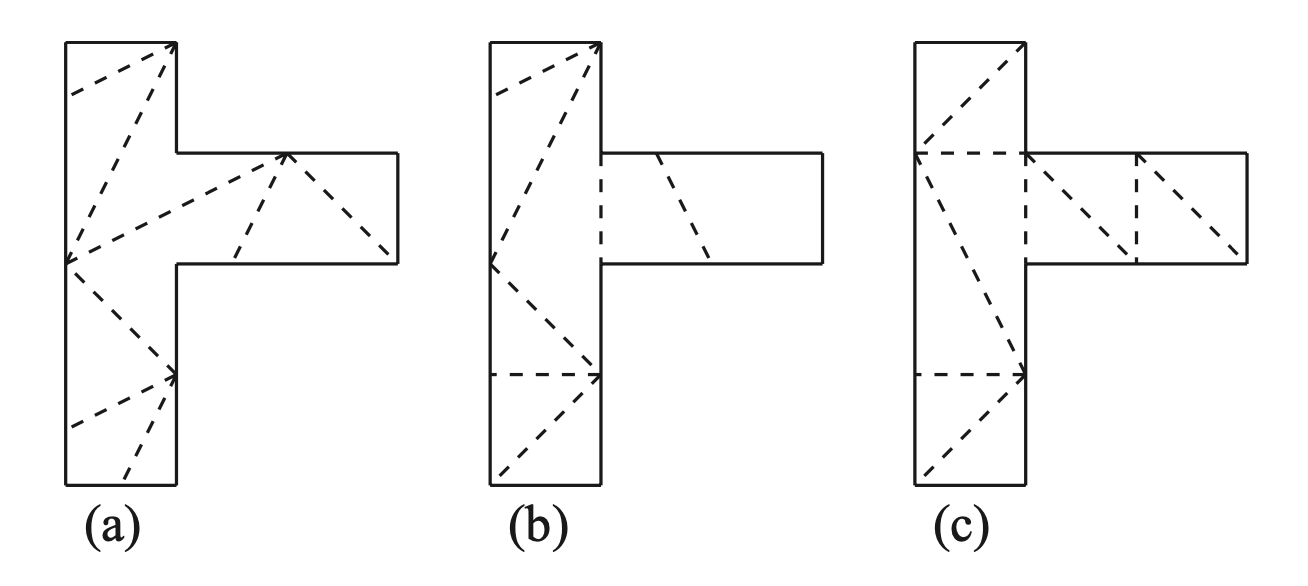
凸多面体から展開図を作る問題の逆問題として、平面図形(平面多角形)から凸多面体を作る問題があります。
展開図からは多面体は一つしかできないと思われがちですが、一つの平面多角形から折り目を取り替えることで多数の凸多面体が作られる例がいくつも知られています。
この問題を解くにあたっては、平面多角形のどの辺とどの辺を接着(貼合せ)するかを、一定の条件のもとで、コンピュータを用いてシラミ潰しに探索する必要があります。
そのようなアルゴリズムとしては、容易に実装できるが一部分の接着しか探せない辺辺接着アルゴリズムと、すべての接着を探し出す一般接着アルゴリズムがあります。
また、平面多角形の形によって、凸多面体が有限個しかできない場合と、無限個の凸多面体ができる場合があります。
凸多面体が無限にあるのか有限個だけなのかには、「回転ベルト」の存在が関わっています。
この論文ではその有限・無限の判定に関わる重要な定理としての「半分長定理」を証明しています。
次のリンクから論文を見ることができます。