 料理・お酒
料理・お酒 筍と小鮎で夕食
だんだん春らしくなってきました。ということで、昨日の夕食は春らしい食材を買って調理してみました
こないだまでは掌サイズしかなかった筍ですが、ひとまわり大きい愛媛産を見つけました。値段の方はまだ高めです。その4分の1をオリーブ焼きにし...
 料理・お酒
料理・お酒  旅行・散歩
旅行・散歩  折り紙の数学
折り紙の数学  数学
数学 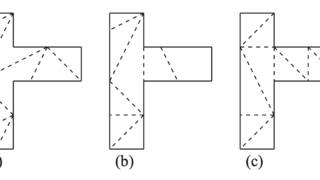 折り紙の数学
折り紙の数学  数学
数学 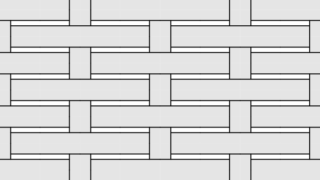 数学
数学  旅行・散歩
旅行・散歩 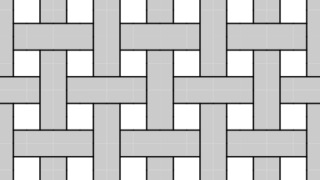 数学
数学 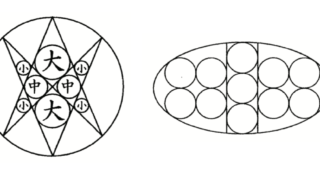 和算
和算