これは2023年10月の論文です
松山大学創立100周年記念論文集, (2023) pp. 51–72.
論文の「はじめに」の部分を引用して論文紹介とします。
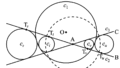
算変座標は、複数の円が互いに接している和算問題への応用を目指し、論文「算変法不変式がつくる座標系について」で定義した円を決定する座標系である。その座標系を用いると、2円が接する条件は距離公式により式に表すことができ、円の半径は算変座標が決まれば半径公式から得ることができる。その後の論文「算変座標の杉成算への応用」では、和算の中でも難問として知られる杉成算の問題に算変座標を適用し、\(n=7\) の場合の杉成算を解くことができた。また論文「算変座標の基礎(1)」では、算変座標の理論的基礎づけを一般メビウス変換の視点から\(\sigma > 0\) の場合について詳細に調べあげた。
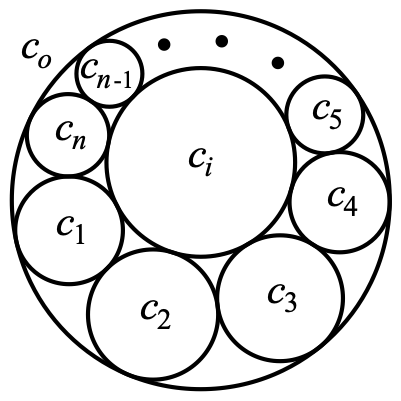
この論文では、シュタイナー円鎖が関わる和算の問題への算変座標の応用について検討する。ちょうど「『累円術無寄』について — 算変座標で解く—」の延長線上に位置づけられる内容となっている。算変座標に関する用語や記号はこれまでの3つの論文で述べたものをこの論文でも使用する。
この論文はここからダウンロードできます。