立体図形
立体図形(凸多面体)は頂点、辺、面という構成要素からなっています。
立体図形の辺のことを昔は「稜(りょう)」と呼んでいました。
例えば、立方体の場合は、頂点が8個、辺が12個、面が6個からなっています。
展開図を作る
それでは立方体の展開図を作ってみましょう。辺にハサミを入れて切り開いて、平面の上に広げます。広げたようすを図にしたのが展開図です。
展開図は一つとは限りません。例えば、立方体の展開図は11通りもあります。
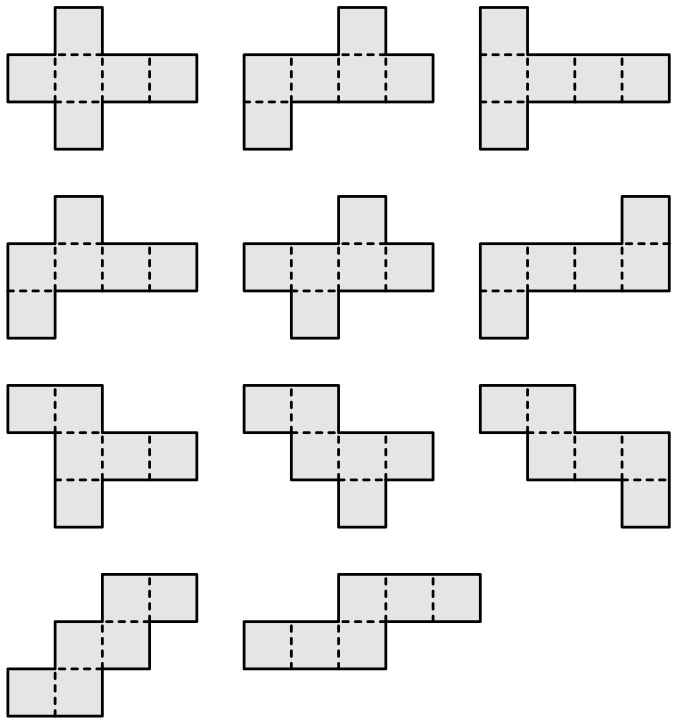

たくさんあるんだね。形がみな違うね。

形が違っていても、共通な性質もあるんだよ。
辺が12個あるなかで、展開図に開くときに「ハサミを入れる辺の個数」は何個かな ?
それから、「ハサミを入れない辺の個数」は何個かな ?
ハサミを入れない辺の個数

ハサミを入れない辺は、展開図に残っている点線でかかれた辺だよね。

そうだよ。

どの展開図も5本だね。

展開図はたくさんあるけど、ハサミを入れない辺の個数は一定なんだよ。
展開図の公式 1
展開図の公式 1
ハサミを入れない辺の個数 = 面の個数 – 1

展開図の公式 ? そんな公式、聞いたことがないよ。

そうだと思うよ。私がかってにつけた名前だからね。
次のように考えてみよう。
展開図の中の点線の辺(ハサミを入れていない辺)を1辺ずつハサミで切ってみよう。
- 1回切ると、展開図は2つに分かれる
- 2回切ると、展開図は3つに分かれる
- ・・・
- 5回切ると、展開図は6つに分かれる。
面は6個なので、6つに分かれたら、面はバラバラになったことになる。これ以上切る辺はないので、ハサミを入れていない辺は5個だとわかる。この考え方から展開図の公式1が成り立つ。

この公式はどんな展開図でも成り立つのかな ?

凸多面体の展開図はみなこの公式が成り立つよ。
どんな立体(凸多面体)の展開図もこれ以上切ったら1つにまとまった形にはならないギリギリのところまでハサミを入れて作っているから、展開図にさらにハサミを入れるたびに2つ、3つと別れることは立方体のときと同じだよ。
でも、きちんと証明しようとするとたいへんだけどね。
ハサミを入れる辺の個数
今度は、ハサミを入れる辺の個数について考えてみよう。

ハサミを入れる辺の個数とハサミを入れない辺の個数を足し合わせると、辺全体の個数になるよね。

そうだね。でも別の見方もできるよ。頂点の数との関係はどうなるかな。
次の図は、先ほどの11個の展開図それぞれについて、ハサミを入れる辺に赤い色を塗ってみました。
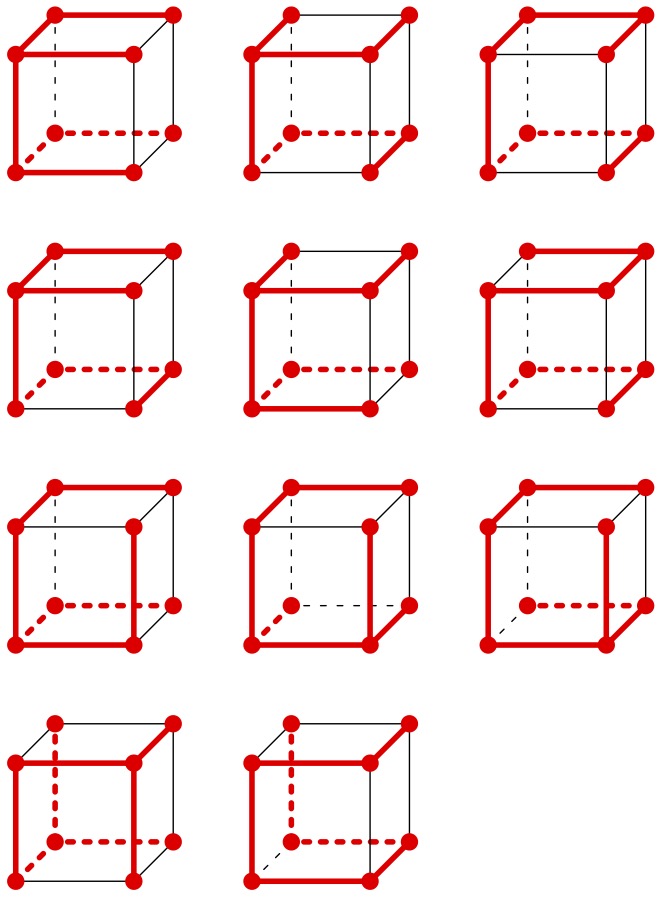

なんだか難しそう。でも、8個の頂点が赤い線で全部つながっているね。

他にも特徴があるよ。
- すべての頂点がハサミを入れる辺(赤い辺)でつながっている
- ハサミを入れる辺(赤い辺)には閉路(輪になっている道)がない
つぎの例で考えてみよう。
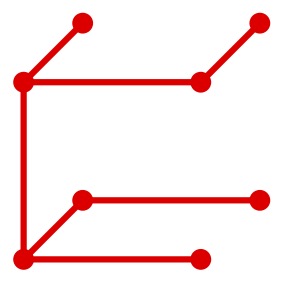
この図では、8個の頂点が赤い辺で1つにつながっている。赤い辺を1個ずつ取り除いてみよう。
- 辺を1つ取り除くと、2つに別れる
- 辺を2つ取り除くと、3つに別れる
- ・・・
- 辺を7つ取り除くと、8つに別れる
頂点は8個なので、辺を7つ取り除くと、8個の頂点がバラバラになったことになる。これで赤い辺(ハサミを入れる辺)の個数は7個ということがわかる。この考え方をまとめてみると…。
展開図の公式 2
展開図の公式 2
ハサミを入れる辺の数 = 頂点の数 – 1

この公式もどんな展開図でも成り立つのかな ?

公式 1 のときと同じだよ。凸多面体の展開図はどれでもこの公式が成り立つよ。
でも、きちんとした証明をしようとすると、これも大変だけどね。

展開図がたくさんあっておどろいたけど、どの展開図にも共通な性質が2つもあったんだね。

まだあるよ。2つの公式を足し合わせたらどうなるかな。
オイラーの多面体定理

とても有名な定理になるよ。
オイラーの多面体定理
辺の数 = 頂点の数 + 面の数 – 2

この定理はどんな立体でも成り立つのかな。

ここでは展開図の公式を使ってみちびいたから、この説明だと展開図がある多面体だけということになるけど…。

でも、展開図のあるなしにかかわらずこの多面体定理が成り立つことが証明されているよ。